QUADRIQUES

QUADRIQUES

Les surfaces de l’espace matériel, que nous connaissons par leur emploi, en architecture par exemple, étaient autrefois classées en «corps ronds» et «corps droits». La sphère et le cube sont des surfaces typiques de ces deux familles.

Les corps ronds sont, essentiellement, la sphère déjà citée, le cylindre et le cône usuels (fig. 1). Étudiées individuellement, ces surfaces semblent n’avoir que peu de points communs: l’une est bornée, les deux autres ne le sont pas. Le cône possède un point remarquable (son sommet), alors que le cylindre est totalement homogène. Il est toutefois bien connu que les intersections de ces trois surfaces par des plans sont toujours des coniques , éventuellement dégénérées en couples de droites. L’adjectif conique, c’est-à-dire dessiné sur un cône, est à l’origine du nom donné à ces courbes ^{[cf. CONIQUES]}.

Les propriétés très remarquables des coniques, qui constituent l’ensemble le plus riche de courbes simples, avaient conduit les Grecs à unifier partiellement les définitions et les démonstrations propres à chacune d’elles (ellipse, parabole et hyperbole). Seule la géométrie analytique cartésienne, pourtant, a permis de donner des coniques la définition essentielle: ce sont les courbes algébriques du second ordre , c’est-à-dire les ensembles de points dont les coordonnées (x , y ) satisfont à une égalité de la forme:

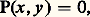où P est un polynôme non nul du second degré. Suivant la nature des nombres x et y (qui sont réels ou complexes), on définit plusieurs types de coniques.

La généralisation de cette notion à l’espace de dimension trois est alors évidente. Les surfaces ainsi définies sont appelées quadriques . Leurs sections planes sont des coniques; et cela les caractérise évidemment parmi les surfaces algébriques.

1. Cadre naturel de la théorie

Extensions diverses

Une quadrique est un ensemble de points satisfaisant à une égalité de la forme suivante où l’un au moins des six premiers coefficients n’est pas nul: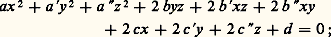

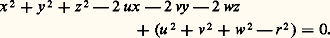par exemple, une sphère (dont le centre a pour coordonnées u , v et w ) a une équation du type:

Certaines complications dans la théorie de ces surfaces conduisirent les mathématiciens du XIX^e siècle à étendre, dans deux directions différentes, la notion de quadrique et des autres surfaces algébriques. Non seulement ils firent un usage systématique des coordonnées complexes, enrichissant ainsi considérablement le modèle mathématique issu des corps de l’espace matériel, mais ils élargirent le concept de point en considérant des «éléments à l’infini» par l’introduction d’une quatrième coordonnée t , nulle pour les nouveaux points.

Pour ces géomètres, une quadrique était donc finalement déterminée par une équation de la forme:

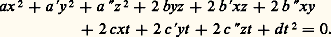Les «points» de ces quadriques sont, en réalité, non des points d’un espace classique (dit affine , de dimension trois sur le corps des nombres réels), mais des droites d’un espace vectoriel de dimension quatre sur le corps des nombres complexes. L’ensemble de ces droites, c’est-à-dire des sous-espaces vectoriels de dimension 1, est appelé le projectifié complexifié de l’espace usuel.

Cette extension donna une grande unité aux théorèmes: ainsi, une droite arbitraire coupe toujours une quadrique en un point au moins. Dans ce cadre, une théorie fort élégante de la polarité, directement généralisée à partir de considérations analogues sur les coniques, conduit à un grand nombre de propriétés (sur les plans tangents, par exemple), pour lesquelles on n’est plus tenu de distinguer un grand nombre de cas.

Quadriques et formes quadratiques

Ce passage d’un espace affine à un espace projectif – au prix d’une augmentation de la dimension – permit surtout de placer la théorie des quadriques dans son véritable cadre: celui des formes quadratiques . Conformément à une tendance actuelle, l’étude détaillée des coniques et des quadriques est aujourd’hui délaissée au profit de la notion plus générale d’hyperquadrique , définie comme un ensemble de droites vectorielles d’un espace E sur un corps algébriquement clos de caractéristique différente de deux; une droite appartient à cet ensemble si et seulement si les vecteurs qui la composent annulent une forme quadratique non nulle q . L’égalité:

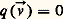est une équation de l’hyperquadrique.

Cette généralisation est parfaitement typique de l’algébrisation d’une théorie géométrique; en quelques pages, toutes les notions de conjugaison et leurs cas particuliers (hyperplans tangents ou symétries centrales, par exemple) peuvent être étudiés comme applications de la théorie de la conjugaison de vecteurs par rapport à la forme q .

Donnons un exemple: pour que deux points donnés, associés à deux vecteurs et de l’espace E, forment une division harmonique avec deux points de l’hyperquadrique, il est nécessaire – et suffisant en général – que l’on ait l’égalité:

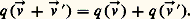Dans le cas particulier – évidemment très utile – où l’espace E est de dimension finie, le calcul matriciel permet une traduction souple des calculs analytiques. C’est ainsi que l’équation d’une quadrique classique peut s’écrire:

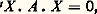où X est la matrice colonne composée des quatre nombres x , y , z et t ; ^t X est la matrice ligne transposée de la précédente, et A une matrice symétrique réelle:

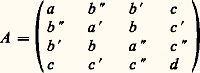Une quadrique est dite propre si la forme quadratique associée q est non dégénérée, ce qui se traduit par le fait que le déterminant = det A de la matrice A est non nul. Si = 0, la quadratique est dite impropre .

2. Quadriques impropres

Il existe onze types différents de quadriques impropres, parmi lesquels on distingue trois familles principales: les cônes, les cylindres et les quadriques décomposées.

Cônes

Les cônes sont obtenus à partir d’un sommet et d’une base, conique non décomposée dont le plan ne contient pas le sommet. Le cône de révolution est l’un d’eux; on peut l’engendrer par rotation d’une droite autour d’une droite fixe qu’elle rencontre: un cône est constitué de deux nappes, c’est-à-dire de deux parties symétriques limitant des volumes convexes et reliées entre elles par le sommet commun (fig. 2).

Le sommet d’un cône est toujours réel. C’est le seul point de cette espèce si la conique de base est totalement non réelle; le cône est alors dit imaginaire. Sinon, le cône est réel, et la nature de la conique de départ est sans importance.

Cylindres

Les cylindres sont des cônes dont le sommet est «à l’infini»: ils sont donc obtenus par des droites (génératrices) ayant une direction donnée qui rencontrent une conique non décomposée dont le plan n’est pas parallèle à la direction. Là aussi, le cylindre de révolution (qui sert de base à tant d’éléments architecturaux) en est l’exemple le plus simple.

Suivant que la conique est non réelle, ou une ellipse, ou une hyperbole, ou une parabole, le cylindre est dit imaginaire, elliptique, hyperbolique ou parabolique (fig. 3). Le cylindre de révolution est un cas particulier de cylindre elliptique. Les sections planes sont, en général, des coniques de même genre que la conique de base.

Quadriques décomposées

Les couples de plans sont des quadriques à la fois impropres et décomposées ; ce dernier qualificatif signifie simplement qu’il s’agit alors de la réunion de surfaces algébriques d’ordre inférieur à celui de la quadrique: ce sont donc des plans. Il en existe cinq sortes, selon que les deux plans sont réels et sécants, réels et parallèles, non totalement réels (mais transformés l’un en l’autre par une conjugaison des coordonnées) et sécants, non réels et parallèles, ou réels et confondus.

Pour qu’une quadrique soit décomposée, il est nécessaire et suffisant que l’on puisse écrire l’égalité:

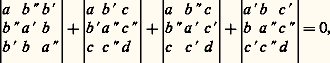et que la quadrique soit impropre. Pour qu’elle soit décomposée en un plan double, il s’introduit une condition supplémentaire: l’ensemble des deux premières conditions est équivalent au fait que 0 doit être une valeur propre au moins double de la matrice A ; la troisième condition entraîne que 0 est alors une valeur propre au moins triple.

3. Quadriques propres

Les quadriques propres présentent moins de variété. Elles se classent également en trois familles (ellipsoïdes, hyperboloïdes et paraboloïdes) ayant chacune deux sous-familles.

Ellipsoïdes

Les ellipsoïdes (fig. 4), par un changement d’axes approprié, peuvent se mettre sous la forme:

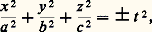où a , b et c sont des nombres réels et strictement positifs. Le signe moins correspond à un ellipsoïde imaginaire, dont aucun point n’a toutes ses coordonnées réelles. Le signe plus correspond à l’ellipsoïde classique dont la partie réelle équivaut, grosso modo, à une sphère, surface en laquelle on peut le transformer par des affinités appropriées (de la même façon que l’on transforme une ellipse réelle en un cercle). Il est de révolution si deux des nombres a , b et c (b et c , par exemple) sont égaux; on le qualifie de sphérique si a = b = c , d’aplati si a 麗 b =c , d’allongé si a 礪 b = c .

Les sections planes d’un ellipsoïde sont en général des ellipses, réelles ou non.

Hyperboloïdes

Les hyperboloïdes ont une équation que l’on peut mettre sous l’une des deux formes suivants:

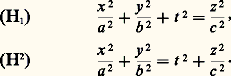Le premier cas est celui de l’hyperboloïde à une nappe (fig. 5), qui est une surface connexe évoquant la forme d’une bobine. On peut le considérer, de deux façons différentes, comme réunion d’une famille de droites, les génératrices. Une affinité convenable, qui revient à égaler les coefficients a et b , le transforme en hyperboloïde de révolution, engendré par la rotation d’une droite autour d’une droite qu’elle ne rencontre pas.

Les sections planes sont des coniques de toutes espèces; un plan tangent coupe l’hyperboloïde suivant deux droites sécantes, qui le séparent en deux parties situées de chaque côté de ce plan.

Le second cas est celui de l’hyperboloïde à deux nappes (fig. 6), qui admet deux nappes disjointes, connexes, limitant deux volumes convexes. Les génératrices d’une telle surface ne sont pas réelles, sauf éventuellement en leur point commun.

Paraboloïdes

Les paraboloïdes ont une équation que l’on peut mettre dans l’une des deux formes suivantes:

où p et q sont deux nombres réels non nuls.

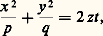Si p et q sont de même signe, le paraboloïde est elliptique (fig. 7), de révolution si p = q . Une affinité convenable peut toujours mettre le paraboloïde sous cette forme; la surface résulte alors de la rotation d’une parabole autour de son axe.

Les sections planes sont des paraboles ou des ellipses. Dans le cas d’un paraboloïde de révolution, une section plane se projette sur un plan orthogonal à l’axe suivant une droite ou un cercle.

Si p et q sont de signes différents, le paraboloïde est hyperbolique (fig. 8). C’est une surface assez remarquable, dont la forme évoque celle d’une selle de cheval.

Une quadrique propre possède, comme nous l’avons vu à propos de l’hyperboloïde à une nappe, un double système de génératrices. Dans le cas du paraboloïde hyperbolique, les génératrices passant par un point réel sont réelles; elles séparent la surface en deux parties situées de part et d’autre du plan tangent. Les sections planes sont des paraboles ou des hyperboles.

Le paraboloïde hyperbolique possède de nombreuses définitions géométriques très simples. Citons-en deux:

– Si l’on se donne trois droites soumises à la seule condition d’être parallèles à un même plan, une droite variable qui rencontre ces trois droites engendre un paraboloïde hyperbolique;

– Si l’on se donne deux droites quelconques, une droite variable qui les rencontre toutes les deux et reste parallèle à un plan donné engendre un paraboloïde hyperbolique.

Les plans apparaissant dans l’une ou l’autre de ces définitions sont appelés plans directeurs de la surface. Il en existe deux, définis chacun à une translation près.

Les ellipsoïdes et les hyperboloïdes ont, à la fois, un centre et des plans de symétrie. Les paraboloïdes n’ont que des plans de symétrie.

4. Problèmes tangentiels

Les dix-sept variétés de quadriques donnent une idée assez complète des différentes formes que peuvent prendre les surfaces de l’espace usuel. Paraboloïde hyperbolique et hyperboloïde à une nappe fournissent des exemples très simples de surfaces qui traversent leurs plans tangents (ce qui n’est pas le cas de la sphère ou du cylindre de révolution, par exemple).

Une étude assez simple, fondée sur la théorie des valeurs et des vecteurs propres d’une matrice réelle symétrique, permet de déterminer les plans qui coupent une quadrique suivant des cercles. Ces plans sont parallèles entre eux (on se limite à des plans réels). Certains plans limites sont tangents à la surface en des points appelés ombilics . Il y en a deux pour un ellipsoïde réel non sphérique, deux pour un hyperboloïde à une nappe, deux pour un paraboloïde elliptique. Il existe des cas particuliers; par exemple, tous les points d’une sphère sont des ombilics.

Les quadriques propres sont non seulement des ensembles de points soumis à des conditions du second degré, mais aussi des enveloppes de plans dont les paramètres annulent un polynôme homogène du second degré, autre forme quadratique attachée à la surface. Aussi dit-on que ces quadriques sont des enveloppes de seconde classe . Un cône, par exemple, ne répond pas à cette définition, car il possède deux équations tangentielles au lieu d’une.

Les quadriques généralisent donc étroitement les propriétés affines et projectives des coniques ^{[cf. CONIQUES]}. Il faut noter toutefois que, hormis les quadriques de révolution, obtenues par simple rotation d’une conique autour d’un axe, il n’existe pas de concept analogue à ceux de foyers et de directrices pour les coniques. Ces notions métriques sont donc directement liées à la structure particulière du plan. Sans doute cela provient-il, comme pour la plupart des résultats non généralisables si la dimension de l’espace excède deux, de la structure des rotations planes dont le groupe cesse d’être commutatif lorsque la dimension passe de deux à trois.

Encyclopédie Universelle. 2012.